Kinematika
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Lorentzova transformace
Víme již, že Galileo Galilei odvodil
transformační vztahy mezi
souřadnicemi x, y, z, t události U v
inerciální soustavě K a souřadnicemi x´, y´, z´,
t´ této události v soustavě K ´. Tato transformace je založena na předpokladech
o absolutnosti času (t = t´) a absolutnosti délek (l = l´).
Oba předpoklady jsou
přibližně správné, avšak jen pro rychlosti mnohem menší než rychlost světla c. Proto
ve speciální teorii relativity nahrazujeme Galileiho transformaci obecnějšími rovnicemi,
tzv. Lorentzovou transformací.

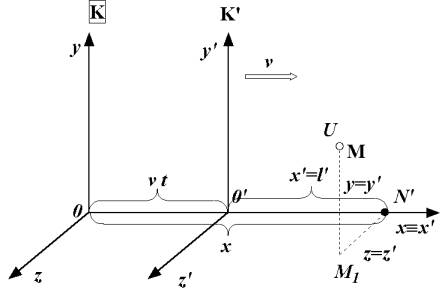
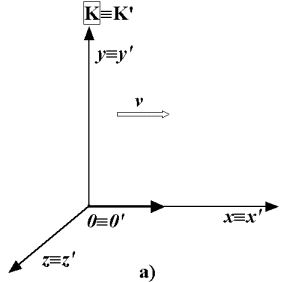
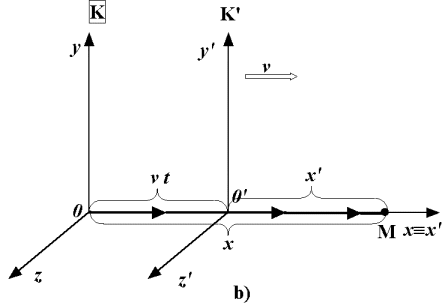
V inerciální soustavě K ´ zvolíme bod N´ ve vzdálenosti l´= x´od počátku
O´ (viz obr.). Úsečka O´N´ o vlastní délce l´ se vzhledem
k soustavě K
pohybuje rychlostí v a její délku l v soustavě K
určíme jako vzdálenost současných poloh obou jejích koncových bodů:
l = x - vt, kde x je souřadnice bodu N´ v čase t a vt
je souřadnice bodu O´ v témže okamžiku. Při libovolných rychlostech
v < c platí relativistický vztah pro kontrakci délek
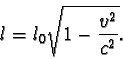
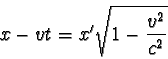
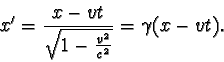
Samozřejmě pro
![]() je
je
![]() a platí
a platí
![]() ,
tzn. vztah Lorentzovy transformace přechází ve vztah Galileiho transformace.
,
tzn. vztah Lorentzovy transformace přechází ve vztah Galileiho transformace.
Vyjdeme-li opět z předchozí situace znázorněné na obrázku a uvažujeme-li úsečky rovnoběžné s osami y´, z´, jsou tyto kolmé ke směru pohybu vztažné soustavy K ´ a kontrakce délek zde tedy nenastává. Proto pro transformaci souřadnic y´, z´ platí ve speciální teorii relativity stejné rovnice jako v Galileově transformaci y´= y a z´= z.
 |
 |
Při odvození vztahu pro časovou souřadnici vyjdeme z principu
konstantní rychlosti světla. Předpokládáme, že v čase t = t´= 0,
ve kterém
se souřadnicové osy obou soustav kryjí, vyšle pozorovatel v soustavě K světelný
signál v kladném směru osy x. Za dobu t dospěje světlo do bodu o souřadnici
x = ct. Tato událost má v soustavě K souřadnice x a t.
V soustavě K ´ urazí světlo dráhu x´= ct´ a tato událost bude mít souřadnice
x´ a t´.
Z obou uvedených rovnic a ze vztahu pro transformaci souřadnice x dostáváme
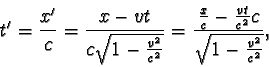
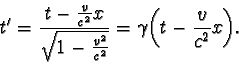
Tato rovnice se nazývá Lorentzův vztah pro transformaci času . Pro
![]() lze zanedbat výraz
lze zanedbat výraz
![]() vzhledem k číslu 1 a výraz
vzhledem k číslu 1 a výraz
![]() vzhledem k t, čímž dostáváme
vzhledem k t, čímž dostáváme
![]() .
To je opět výraz odpovídající Galileově transformaci.
.
To je opět výraz odpovídající Galileově transformaci.
Lorentzova transformace
Pro rychlosti v mnohem menší než je rychlost světla ve vakuu c samozřejmě celá Lorentzova transformace přechází v transformaci Galileovu, jejíž důsledky můžeme při těchto rychlostech považovat za správné i z pohledu speciální teorie relativity.
Z transformačního vztahu pro časovou souřadnici lze také odvodit relativnost současnosti dvou nesoumístných událostí, neboť tento výraz v sobě obsahuje i souřadnici x. Při výpočtu časové souřadnice t´ musíme tedy znát nejen čas t, ale i x-ovou souřadnici místa, v němž se tato událost odehrála. Událostem, které nastaly ve stejném čase t ve dvou odlišných bodech např. na ose x soustavy K, proto odpovídají dvě různé časové souřadnice v soustavě K ´. Podobně lze z transformačních rovnic odvozovat i další důsledky, které jsme si již odvodili. Při tomto postupu se Lorentzova transformace odvodí ihned po formulaci základních principů podobně jako to učinil sám A. Einstein.
Příklady k lepšímu pochopení - Příklady k procvičení
Začátek stránky
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Speciální teorie relativity, Jaroslav Joch © 2000