Kinematika
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Podélný Dopplerův jev
Závislost frekvence vlnění, kterou vnímá pozorovatel, na vzájemné rychlosti zdroje vlnění a pozorovatele, objevil v roce 1842 rakouský fyzik Ch. Doppler (1803 - 1853), a proto ji nazýváme Dopplerův jev. Jestliže vzájemný pohyb zdroje a pozorovatele probíhá ve směru šíření vlnění, nastává podélný Dopplerův jev. Každý jistě známe z vlastní zkušenosti situaci, kdy projíždíme ve vlaku kolem výstražné signalizace na přejezdu nebo kolem nás projíždí houkající lokomotiva. Při přibližování je tón vyšší a naopak, když se zdroj zvuku vzdaluje tón se sníží.
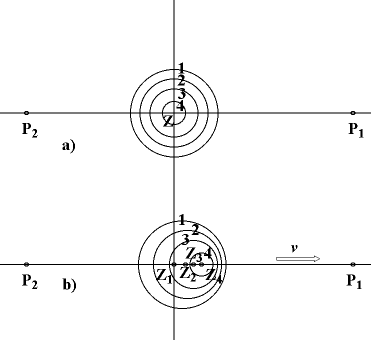
Podstatu Dopplerova jevu lze názorně vyjádřit pomocí jednoduchého schematu. Na prvním
obrázku vidíme vlnoplochy, které vysílá nepohybující se zdroj ve čtyřech po
sobě následujících periodách T0. Pozorovatelé P1
i P2 zjišťují přitom stejnou vlnovou
délku l0, jakou vysílá zdroj vlnění. Na druhém obrázku
jsou znázorněny vlnoplochy, které vysílá zdroj vlnění o stálé frekvenci
n0, který se blíží
rychlostí v ve směru Z1P1
k pozorovateli P1. Tento pohybující se zdroj vyslal vlnoplochu 1
z bodu Z1, vlnoplochu 2 z bodu Z2, který má
od bodu Z1 vzdálenost vT0, vloplochu 3 z bodu
Z3, jehož vzdálenost od místa Z2 je
vT0, atd. Je jasné, že směrem k pozorovateli P1
jsou vlnoplochy zhuštěny, tj. vlnová délka
l je o vT0 kratší, než kdyby byl zdroj
v klidu. Směrem k pozorovateli P2 jsou vlnoplochy dále od sebe
a pozorovatel P2 tedy přijímá vlnění o vlnové délce větší
o vT0, než kdyby byl zdroj v klidu.

Vztah mezi frekvencí vlnění n, kterou přijímá pozorovatel
P1 od pohybujícího se zdroje Z, a frekvencí
n0 téhož zdroje nacházejícího se
vzhledem k pozorovateli v klidu si nejprve vyjádříme klasicky.
Rychlost vlnění označíme c. Pro vlnovou délku lambda přijímanou
pozorovatelem P1 od pohybujícího se zdroje vlnění pak platí
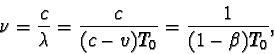
Podle speciální teorie relativity má podélný Dopplerův jev stejnou příčinu, jako v klasické fyzice, navíc se zde však ještě uplatňuje relativistická dilatace času. Perioda T0 zdroje vlnění v klidu zde totiž sovisí s periodou T zdroje pohybujícího se rychlostí v, vztahem
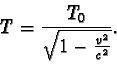
Vlnová délka l, kterou přijme pozorovatel P1, k němuž se zdroj vlnění přibližuje, je proto
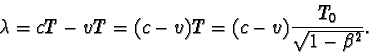
Frekvenci n, kterou přijímá pozorovatel P1,
lze pak vyjádřit vztahem
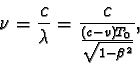
resp. vztahem
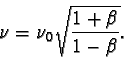
Relativistický vztah pro Dopplerův jev byl potvrzen např. měřením frekvence světla vysílaného rychle se pohybujícími vodíkovými ionty. Jeho hlavní význam však spočívá v astronomických měřeních relativního pohybu kosmických objektů, který se projevuje změnou frekvence jimi vysílaného světla. Z posunu spektrálních čar ve spekterch těchto objektů se pak určuje jejich rychlost vzhledem k Zemi.
Začátek stránky
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Speciální teorie relativity, Jaroslav Joch © 2000