Kinematika - Michelsonův pokus

Je jedním z nejznámějších pokusů vedoucích ke speciální teorii relativity. Zabývá se měřením rychlosti světla v různých směrech vzhledem k Zemi. V 19. století fyzikové předpokládali, že tato rychlost je v různých směrech různá, a snažili se toho využít k určení absolutního pohybu Země. (V té době se totiž předpokládala existence nějakého nosného prostředí pro optické vlnění, nazvaného světelný éter.)

Již v roce 1881 provedl americký fyzik A. A. Michelson (1852 - 1931) optický pokus, kterým chtěl zjistit absolutní pohyb Země vzhledem k éteru. Neměřil ovšem přímo rychlost světla, ale pouze dráhový rozdíl dvou světelných paprsků, které se pohybují po dvou stejných dráhách různě orientovaných vůči směru pohybu Země.

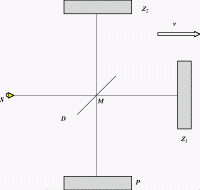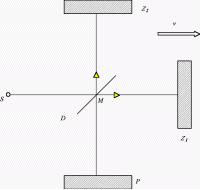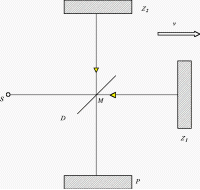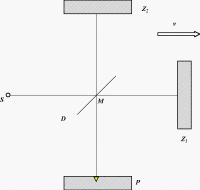
Princip zařízení ukazuje obrázek. Monofrekvenční světlo vyslané zdrojem S dopadá na polopropustnou destičku D pod úhlem 45°. Část světla se šíří dále a po odrazu od zrcátka Z₁ se vrací nazpět k destičce. Na ní se odrazí a dopadne na stínítko P. Druhá část světla se od destičky odrazí kolmo k dopadajícímu paprsku a po odrazu od zrcadla Z₂ a průchodu polopropustnou destičkou také dopadá na stínítko P. Oba světelné svazky jsou koherentní (tzn. mají stálý dráhový rozdíl, neboť pocházejí ze stejného zdroje), a proto vytvářejí na stínítku interferenční obrazec. Použitý přístroj proto nazýváme Michelsonovým interferometrem.

Pro jednoduchost předpokládáme, že rameno MZ₁ je orientováno souhlasně s rychlostí v pohybu Země vzhledem k absolutní vztažné soustavě. Světlo se bude šířit vzhledem k Zemi po obou ramenech MZ₁ a MZ₂ různými rychlostmi, a tedy i doby, za které paprsky dopadnou na stínítko P, se budou lišit.

První paprsek se bude po dráze MZ₁ pohybovat rychlostí c - v a při zpětném pohybu z bodu Z₁ do bodu M rychlostí c + v. Ze známého definičního vztahu pro velikost rychlosti $\begin{displaymath}v = \frac {s}{t} \end{displaymath}$ snadno určíme potřebný čas

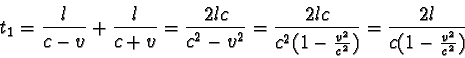
$\begin{displaymath}t_{1} = \frac { l }{ c - v } + \frac { l }{ c + v } = \frac {... ... {v^{2}}{c^{2}})} = \frac {2l}{c (1 - \frac {v^{2}}{c^{2}})} \end{displaymath}$

Druhý paprsek se bude po dráze MZ₂ šířit v obou směrech stejnou rychlostí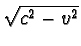

, kterou dostaneme vektorovým složením obou rychlostí c a -v. Danou dráhu 2l tedy urazí za dobu

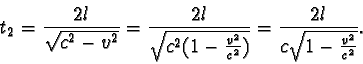
$\begin{displaymath}t_{2} = \frac { 2l }{ \sqrt {c^2 - v^2} } = \frac {2l}{ \sqrt... ...{c^2}) } } = \frac {2l}{c \sqrt {1 - \frac {v^2}{c^2} } } . \end{displaymath}$

Z výsledků vidíme, že paprsek pohybující se ve směru pohybu Země urazí danou dráhu za delší čas. Na stínítku tedy vzniká vlivem dráhového rozdílu interferenční obrazec v podobě soustředných kroužků. Při libovolném otočení celého zařízení by se měl tento obrazec změnit. To se však nikdy nestalo, ačkoliv Michelson se svým spolupracovníkem Morleyem tento pokus mnohokrát opakoval s ještě přesnějším zařízením. Stejný výsledek dostáváme i v současnosti při měřeních, která by zaregistrovala pohyb Země o rychlosti pouhých 5 m.s^-1. (Skutečná oběžná rychlost Země okolo Slunce je 30 km.s^-1.)