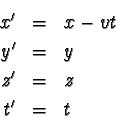
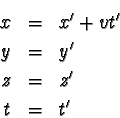
Kinematika
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Galileiho transformace
Transformační rovnice nám umožňují pomocí souřadnic x, y, z, t nějaké události U v inerciální vztažné soustavě K vyjádřit souřadnice x´, y´,z´ a t´ téže události v jiné inerciální vztažné soustavě K ´, která se vzhledem k původní soustavě K pohybuje rychlostí v.
Při odvození předpokládáme, že v čase t = t´= 0 souřadnicové osy obou
soustav splývají. Inerciální soustava K ´ se pak pohybuje ve směru osy x
konstantní rychlostí v tak, že osa x´ při tomto pohybu splývá
s osou x a osy y´,z´ jsou rovnoběžné s osami y a z.
Transformační rovnice pro přechod od soustavy K k soustavě K ´
(resp. od soustavy K ´ ke K) mají v tomto případě podobu:
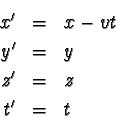
|
resp. | 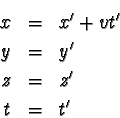
|
Tyto rovnice nazýváme Galileiho transformační rovnice nebo zkráceně
jen Galileiho transformace.
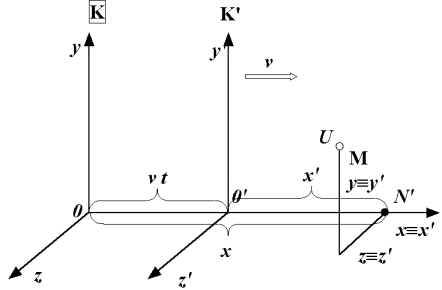
Při pohledu na obrázek a předchozí úvahy se jeví odvození Galileiho transformace zcela přirozené, avšak ve skutečnosti je založeno na dvou předpokladech, které tak úplně samozřejmé nejsou.
Příklady k lepšímu pochopení - Příklady k procvičení
Začátek stránky
předchozí - Obsah - další
Úvodní pojmy - Mechanický princip - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Podélný Dopplerův jev - Příčný Dopplerův jev - Hodiny v letadle - Mezony pí - Kontrakce délky - Transformace - Skládání rychlostí
Speciální teorie relativity, Jaroslav Joch © 2000