Příklady k pochopení
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Lorentzova transformace
1.
V čase t´= 2,0.10-5 s od okamžiku, kdy se souřadnicové osy
inerciálních
soustav K a K ´ ztotožnily, vznikla v bodu o souřadnicích
x´= 2,4.103 m, y´= 15 m a z´= 30 m jiskra. Jaké jsou
souřadnice této události v soustavě K, pohybuje-li se soustava K ´
vzhledem k soustavě K v kladném směru osy x rychlostí o velikosti
v = 0,8c ?
Řešení
Pro rychlost v = 0,8c je Lorentzův koeficient
g = 1,667. Dosazením do
Lorentzovy transformace
2.
V inerciální soustavě K je podél osy x rozmístěno pět
synchronizovaných
hodin H1 až H5 ve stejných vzdálenostech
l = 1 m od sebe, přitom prostřední
hodiny jsou v počátku soustavy souřadnic K. Hodiny ukazují stejný čas t = 0 s.
Jaký čas t´ ukazují hodiny H´1 až H´5 rozmístěné
podél osy x´ inercialní
soustavy K ´ tak, aby ležely proti hodinám v soustavě K?
Předpokládáme, že soustava K ´ se pohybuje vzhledem k soustavě K v kladném
směru osy x rychlostí v = 0,98c.
Řešení
Údaje hodin H´1 až H´5 vypočteme ze čtvrté rovnice
Lorentzovy transformace,
do níž dosadíme za čas t = 0 a za souřadnici x postupně
x1 = -2l, x2 = -l, x3 = 0,
x4 = l a x5 = 2l, Lorentzův koeficient
![]() .
Po dosazení dostáváme
.
Po dosazení dostáváme
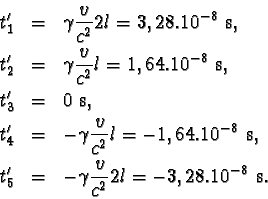
3.
Na ose x inerciální soustavy K vznikly v bodech A a B dvě
současné události U1 a U2. Jaký je časový interval
Dt´ mezi těmito událostmi z hlediska pozorovatele
v soustavě K ´, která se pohybuje vzhledem k soustavě K
rychlostí v?
Řešení
Označme souřadnice obou událostí v soustavě K x1, t1 a x2,
t2; v soustavě K ' x'1, t'1 a x'2, t'2.
Z Lorentzovy transformace pak vyplývá
4.
V předcházejících kapitolách jsme viděli, že některé veličiny jsou relativní, tj.
závisí na volbě inerciální vztažné soustavy. Dokažte pomocí
Lorentzovy transformace, že veličina
c2Dt2 -
l2
kde Dt je časový interval mezi dvěma událostmi
a l vzdálenost mezi
body, v nichž tyto události nastaly, nezávisí na volbě inerciální vztažné soustavy.
Řešení
Předpokládejme, že událost U1 má v soustavě souřadnic K souřadnice
x1, y1, z1, t1;
událost U2 souřadnice x2, y2,
z2, t2. Souřadnice těchto událostí v soustavě K ´
označme x´1, y´1, z´1,
t´1 a x´2, y´2, z´2,
t´2.
Označme dále v soustavě K
Dx = x2 - x1,
Dy = y2 - y1,
Dz = z2 - z1,
Dt = t2 - t1
a analogicky v soustavě K ´
Dx´ = x´2 - x´1,
Dy´ = y´2 - y´1,
Dz´ = z´2 - z´1,
Dt´ = t´2 - t´1.
Máme dokázat, že
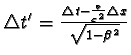 a
a
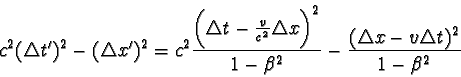
Veličina s definovaná vztahem s2 = c2Dt 2 - l2, kde Dt je časový interval mezi dvěma událostmi a l vzdálenost mezi body, v nichž tyto události nastaly, se nazývá interval mezi uvažovanou dvojicí událostí. Z věty dokázané v tomto příkladu vyplývá, že interval mezi dvěma událostmi je invariantní vzhledem k Lorentzově transformaci, neboli při přechodu mezi inerciálními soustavami pomocí Lorentzovy transformace nemění svoji hodnotu.
5.
Rovnice kulové světelné vlnoplochy vyslané z počátku soustavy souřadnic K
v čase t = 0 je x2 + y2 + z2
= (ct)2. Zjistěte, jaký bude tvar této vlnoplochy v
soustavě K ´, pohybující se vzhledem k soustavě K stálou rychlostí
v. Předpokládejme, že v čase t = t´ = 0 počátky obou soustav
souřadnic K a K ´ splývají.
Řešení
Z rovnice
x2 + y2 + z2 = (ct)2
vyplývá
(ct)2 - (x2 + y2 +
z2) = 0.
Výraz (ct)2 - (x2 + y2 +
z2) = (ct)2 - r2
je interval mezi vysíláním světelného paprsku z počátku soustavy souřadnic K
v čase t = 0 (událost U1) a příchodem světelného paprsku do
libovolného bodu povrchu světelné kulové vlnoplochy o poloměru r v čase t
(událost U2).
Z řešení předcházejícího příkladu vyplývá, že tento interval je invariantní,
platí tedy
(ct)2 - (x2 + y2 + z2) = (ct ´ )2 - (x´ 2 + y´ 2 + z´ 2) = 0.
Z poslední rovnice dostáváme x´ 2 + y´ 2 + z´ 2 = (ct ´ )2; v soustavě K ´ bude tedy světelná vlnoplocha opět kulová.
6.
Vlastní doba života určité nestabilní částice je
Dt0 = 10 ns. Určete
dráhu l, kterou částice proletí od okamžiku svého vzniku do okamžiku
rozpadu v laboratorní vztažné soustavě, ve které doba jejího života je
Dt = 20 ns.
Řešení
Označme symbolem K ´ klidovou vztažnou soustavu částice a symbolem K
laboratorní soustavu, vzhledem k níž se částice pohybuje. Druhá mocnina intervalu
od vzniku do rozpadu částice je v soustavě K rovna:
s2 = c2Dt
2 - l2,
v soustavě K ´:
s´ 2 = c2Dt
02 - l´ 2 =
c2Dt02
(dráha částice l´ v její klidové soustavě K ´ je rovna nule).
Z invariance intervalu pak vyplývá
Příklad lze řešit také pomocí vztahu pro dilataci času.
7.
Dokažte, že časové pořadí událostí, mezi kterými je příčinná souvislost,
je ve všech inerciálních soustavách stejné.
Řešení
Předpokládejme, že v inerciální soustavě K se odehrály dvě události
U1 a U2, přičemž událost U1
je příčinou události U2
(např. výstřel ze zbraně a dopad střely do terče, apod.). Událost U1
(výstřel) má v soustavě K souřadnice x1, t1,
událost U2 (dopad střely do terče) souřadnice x2,
t2. Poněvadž událost U1 je příčinou události
U2 a příčina nastává dříve než její důsledek,
je t2 > t1. Máme dokázat, že v libovolné
inerciální soustavě souřadnic K ´ platí pro časové souřadnice obou událostí
t´1 > t´2.
Ze čtvrté rovnice Lorentzovy transformace vyplývá, že časový interval mezi
oběma událostmi v soustavě K´ je
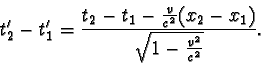
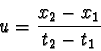
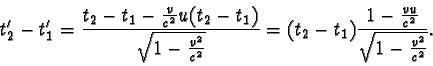
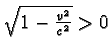 a podle předpokladu
t2 - t1 > 0, dostáváme z poslední rovnice
t'2 - t'1 > 0,
tj.
t'2 > t'1.
a podle předpokladu
t2 - t1 > 0, dostáváme z poslední rovnice
t'2 - t'1 > 0,
tj.
t'2 > t'1.
8.
O speciální teorii relativity má zájem také širší veřejnost. Mnozí lidé
se domnívají, že filosofickým důsledkem speciální teorie relativity je
závěr, že "vše je relativní". Je tento názor správný?
Řešení
Vznik tohoto názoru je pravděpodobně ovlivněn termínem "teorie relativity"
je to však názor nesprávný. Filozofický relativismus ze speciální teorie
relativity nevyplývá a nemá s ní nic společného. Tvrzení, že vše je relativní,
není však správné ani z hlediska fyzikálního. Speciální teorie relativity
sice ukázala, že některé veličiny, považované klasickou fyzikou za absolutní,
jsou ve skutečnosti relativní (např. časový interval nebo délka), na
druhé straně však i v rámci speciální teorie relativity existují veličiny,
které při přechodu od jedné inerciální soustavy k druhé nemění svou hodnotu
(jsou invariantní). Invariantní je např.
rychlost elektromagnetického vlnění (např. rychlost světla) ve vakuu,
která je ve všech inerciálních vztažných soustavách stejná, o této veličině
se klasická fyzika naopak domnívala, že je relativní. Ve speciální teorii
relativity známe také některé další invariantní veličiny.
Ze speciální teorie relativity však vyplývají některé obecnější závěry.
Mezi nejdůležitější patří např. skutečnost, že teorie, která odporuje
našim názorným představám a zdá se být ve sporu s tzv. "zdravým rozumem",
může být ve skutečnosti správná. Einstein se zabýval rozporem mezi našimi
vžitými názorovými představami a pravdivou skutečností také z psychologického
hlediska a označil tzv. "zdravý rozum" za souhrn předsudků, které člověk
získává o okolním světě zpravidla již v mladém věku. Pochopení Einsteinovy
kritiky "zdravého rozumu" je velmi důležité, poněvadž není jen základem
k pochopení teorie relativity, ale i celé moderní fyziky a astrofyziky.
Příklady k procvičení - Lorentzova transformace
Začátek stránky
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Speciální teorie relativity, Jaroslav Joch © 2000