Příklady k pochopení
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Dilatace času
1.
Na kosmické lodi vzdalující se od Země rychlostí 0,1c probíhal určitý děj, který podle
měření účastníků letu trval jednu hodinu. Jak dlouho trvá tento děj pro pozorovatele
na Zemi? Je možné, aby děj trvající na kosmické lodi 1 hodinu trval pro pozorovatele
na Zemi 1 000 000 hodin?
Řešení
Čas Dt0
je vlastní čas trvání děje probíhajícího na kosmické lodi.
Z rovnice
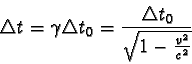
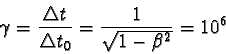
2.
Let letadla pohybujícího se rychlostí 1 000 km.h-1 trval podle
palubních hodin 1 hodinu. Vypočtěte, jak dlouho trval tento let z hlediska
pozorovatele na Zemi.
Řešení
Rychlosti 1 000 km.h
![]() odpovídá Lorentzův koeficient
odpovídá Lorentzův koeficient
![]() .
Ze vztahu
.
Ze vztahu
![]() pak vyplývá,
že děj trvající v letadle 1 hodinu trvá
pak vyplývá,
že děj trvající v letadle 1 hodinu trvá
3.
Při srážkách částic primárního kosmického záření s atomy vrchní vrstvy atmosféry
vznikají miony. Jsou to nestabilní částice se střední dobou života
T0 = 2,2.10-6 s (měřenou v klidové soustavě mionu)
a s hmotností m = 207 me (me je hmotnost elektronu).
Pozorování pomocí stratosférických balónů a raket ukázala, že miony vznikají ve velkých
výškách nad povrchem Země (více než 10 km) a odtud se pohybují k Zemi rychlostí blízkou
rychlosti světla. Za střední dobu života 2,2.10-6 s se mion již rozpadá
na elektron a dvě neutrina.
Předpokládejme, že mion vznikl ve výšce 15 km a pohybuje se k Zemi rychlostí
v = 0,999 8c. Může tento mion doletět na povrch Země?
Řešení
Řešme tuto úlohu ve vztažné soustavě spojené se Zemí. Vzhledem k velké rychlosti
mionu blízké rychlosti světla je třeba při řešení vycházet z principů
speciální teorie reletivity.
Dráha, kterou může mion od okamžiku svého vzniku do okamžiku rozpadu urazit, je
l = vT, kde
![]() je střední doba života mionu v zemské vztažné soustavě.
Poměr rychlosti mionu k rychlosti světla je
b = 0,999 8. Odsud plyne
je střední doba života mionu v zemské vztažné soustavě.
Poměr rychlosti mionu k rychlosti světla je
b = 0,999 8. Odsud plyne
![]() a podle tabulek
a podle tabulek
![]() .
Mion tedy za dobu svého života urazí v zemské vztažné soustavě dráhu
.
Mion tedy za dobu svého života urazí v zemské vztažné soustavě dráhu
Kdyby se neprojevila dilatace času a ten byl absolutní veličinou, pak by nejrychlejší miony mohly do okamžiku svého rozpadu urazit jen dráhu 660 m, a tedy by se nemohly dostávat na povrch Země. V laboratořích na Zemi však můžeme miony vznikající ve velkých výškách běžně zaregistrovat, čímž je opět experimentálně potvrzen jev dilatace času.
4.
Podle studenta zabývajícího se speciální teorií relativity není možné, aby pozorovatel
v soustavě K tvrdil, že hodiny umístěné v soustavě K ´ jdou pomaleji, zatímco
pozorovatel v soustavě K ´ naopak prohlašoval, že pomaleji jdou hodiny umístěné
v soustavěK. V těchto tvrzeních je podle studenta logický rozpor. Zvolíme-li
dvojici navzájem se pohybujících hodin H´ a H1, pak není možné,
aby hodiny H´ pohybující se kolem hodin H1 ukazovaly
menší čas než hodiny H1 (hledisko pozorovatele v K)
a hodiny H1 ukazovaly ve stejném bodě menší čas než hodiny H´
(hledisko pozorovatele v K ´). Např. okamžitá
fotografie musí ukázat, že je správné jen jedno z těchto tvrzení. Pokuste se celý
problém správně vysvětlit.
Řešení
Student má pravdu v tom, že jsou-li vzájemně se pohybující hodiny H´ a
H1 v jednom místě vedle sebe, pak opravdu není možné, aby hodiny H´
ukazovaly menší čas než hodiny H1 a opačně. Správné může být jen jedno
tvrzení. Porovnání údajů obou hodin by tedy vedlo k jednoznačnému závěru.
Avšak jen z porovnání údajů dvou vzájemně se pohybujících hodin na jednom místě (tj. při jejich setkání) nelze vyvodit žádné závěry. Oba pozorovatelé mohli např. ve svých vztažných soustavách uvést své hodiny do chodu v libovolném okamžiku, tzn. mohli nastavit v libovolném okamžiku na svých hodinách H´ a H1 čas t = 0 a t´= 0. Navíc při setkání dvou pohybujících se hodin v jednom místě mohou oba pozorovatelé bezprostředně porovnat jen okamžité údaje obou hodin, z čehož nemohou vyvodit žádný závěr o tom, zda jedny či druhé hodiny jdou vzhledem k určitému pozorovateli např. pomaleji.
Chceme-li z hlediska určitého pozorovatele porovnat chod vzájemně se pohybujících
hodin, musíme nejprve u obou hodin při jejich setkání ve stejném bodě nastavit stejný
čas (např. t = t´= 0) a po uplynutí určité doby jejich údaje opět porovnat.
Po uplynutí této doby však již např. pozorovatel v soustavě K nemůže údaje
obou hodin bezprostředně porovnat, neboť hodiny H´ se mezitím od něj posunuly.
Použije proto další hodiny H2 synchronizované s hodinami H1
nacházející se v bodě, do nějž dospějí hodiny H´ za danou dobu, a pohybující se
hodiny H´ porovná s hodinami H2. Porovnání chodu pohybujících se
hodin H´ s hodinami rozmístěnými v soustavě K vyžaduje tedy celkem
troje hodiny: H1, H2 a H´.
Analogicky pozorovatel v soustavě K ´, který porovnává pohybující se hodiny H1
s hodinami rozmístěnými v soustavě K ´, k tomu opět potřebuje troje hodiny:
H´, H´´ a H1.
Porovnáním údajů hodin H´ a H2 vysloví pozorovatel v soustavě K pak závěr, že hodiny umístěné v soustavě K ´ jdou pomaleji a pozorovatel v soustavě K ´ vysloví na základě údajú hodin H1 a H´´ závěr, že hodiny umístěné v soustavě K jdou pomaleji. Jelikož se však tyto výroky opírají o údaje různých dvojic hodin, není mezi nimi žádný logický rozpor.
5.
Kuře se vylíhne z vajíčka za 21 dní. Předpokládejme, že líheň je umístěna v kosmické lodi
pohybující se vzhledem k Zemi rychlostí v = 0,994c. Jakou dobu vylíhnutí
kuřete zjistí v tomto případě a) kosmonaut na lodi, b) pozorovatel na Zemi?
Řešení
Z principu relativity
vyplývá, že kosmonaut na kosmické lodi zjistí stejnou dobu
líhnutí kuřete, jaká by byla změřena na Zemi, tj. 21 dní. Tato doba je vlastní
čas uvažovaného děje. Doba vylíhnutí kuřete z vajíčka umístěného na kosmické lodi je
pak pro pozorovatele na Zemi určena vztahem
6.
Dvě dvojčata A a B se po oslavě svých dvacátých narozenin rozhodnou, že
dvojče A zůstane na Zemi a dvojče B se vydá na kosmickou cestu ke hvězdě
vzdálené 40 světelných let. U hvězdy se loď hned obrátí a dvojče B se vrátí na Zemi.
Předpokládejme, že kosmická loď se po celou dobu pohybuje konstantní rychlostí 0,99c.
Kolik let bude oběma dvojčatům po návratu kosmické lodi?
Řešení
Při řešení příkladu zvolíme za vztažnou soustavu Zemi. Kosmická loď se vzhledem k ní
pohybuje rychlostí jen o setinu menší, než je rychlost světla. Proto dorazí k hvězdě
přibližně za dobu Dt = 40 let. Na hodinách umístěných
na kosmické lodi uplyne mezi tím menší doba
Dt0,
neboť hodiny pohybující se vzhledem k Zemi jdou z hlediska pozemského pozorovatele
pomaleji. Vlastní čas mezi startem a příletem k hvězdě lze vypočítat ze vztahu
![]() ,
,
z něhož vyplývá
![]()
Při zpětném návratu se hodiny na palubě opět zpožďují a vzhledem k tomu, že se loď
vrací nazpět stejnou rychlostí, trvá návrat podle hodin na Zemi 40 let a podle hodin
na palubě zase jen 5,7 roku. Dilatace času se týká všech přírodních dějů probíhajících
na palubě kosmické lodi včetně jevů biologických. Dvojče B tedy zestárne při kosmické
cestě o 11,4 roku a bude mu po návratu na Zemi 20 let + 11,4 roku = 31,4 roku.
Dvojče A,
které zůstalo na Zemi, zestárne za dobu kosmické cesty o 80 let a v době návratu
jeho sourozence mu tedy bude 20 let + 80 let = 100 let.
Při vyšších rychlostech kosmické lodi může být tento rozdíl samozřejmě ještě mnohem větší.
Tento výsledek je jistě neobvyklý a překvapující, avšak ne nelogický či paradoxní.
Někteří fyzikové se zejména v období vzniku speciální teorie relativity domnívali, že
dojdeme k logickým rozporům, zvolíme-li za vztažnou soustavu kosmickou loď. Pro dvojče
B by pak kosmická loď byla soustavou klidovou a zeměkoule s dvojčetem A by se
od ní nejprve vzdalovala a pak přibližovala rychlostí 0,99c. Protože podle principu
relativity jsou všechny
inerciální vztažné soustavy zcela rovnocenné, vyplývá z
analogických úvah, že by nyní dvojče A umístěné na pohybující se Zemi zestárlo méně
než dvojče B, umístěné na raketě. To je však logický rozpor, neboť jsme uvažovali o
stejném fyzikálním ději z hlediska dvou vztažných soustav, a proto musíme dospět ke
stejnému výsledku. Není možné, aby po přistání rakety na Zemi bylo dvojče A starší než
dvojče B a současně dvojče B starší než A.
Tento paradox, tzv. paradox dvojčat, však vzniká tím, že jsme obě
soustavy nesprávně považovali za inerciální a v důsledku toho jsme také nesprávně tvrdili,
že jsou zcela rovnocenné. Zemi můžeme během letu rakety stále považovat za inerciální
soustavu (zanedbáváme malá zrychlení z vlastních pohybů Země), raketa však musí
nejdříve odstartovat, u hvězdy se zastavit a opět se vrátit zpět. Při tom se pohybuje
zrychleně, a proto není inerciální vztažnou soustavou. Proto také předpoklad v předešlé
úvaze, že kosmická loď je stále inerciální soustava, je nesprávný. Správné zústává pouze
první řešení.
7.
Astronomické objekty nazývané kvasary se vyznačují velkým posuvem spektrálních čar směrem
k červenému konci spektra. U jistého kvasaru bylo měřením zjištěno, že frekvence příslušná
určité čáře jeho spektra se zmenšila v porovnání s frekvencí téže čáry, kterou by vysílal
nepohybující se zdroj světla, třikrát. Určete, jakou radiální rychlostí se vzdaluje
tento kvasar od Země.
Řešení
Mezi frekvencemi n a n0
platí vztah pro podélný Dopplerův jev
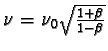 a dále vztah
a dále vztah
![]()
Odtud po úpravě dostáváme
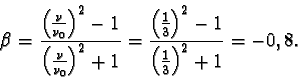
Posuv spektrálních čar k delším vlnovým délkám způsobený Dopplerovým jevem se nazývá rudý posuv. Rudý posuv astronomických objektů ukazuje, že náš vesmír se rozpíná.
Příklady k procvičení - Dilatace času
Začátek stránky
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Speciální teorie relativity, Jaroslav Joch © 2000