Příklady k pochopení
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Úvodní pojmy
1.
Železničář na konci rozjíždějícího se vlaku rozsvítí dvakrát za sebou na velmi krátkou dobu
signální lampu. Vysvětlete, jak změří dobu, která uplyne mezi těmito záblesky, pozorovatel
na trati, který používá k měření nepohyblivé hodiny vzhledem k Zemi.
Řešení
Pro pozorovatele ve vlaku nastávají oba záblesky na témže místě, a proto pro změření časového
intervalu mezi nimi potřebuje tento pozorovatel jen jedny hodiny umístěné v místě záblesků.
Pro pozorovatele na trati začíná děj v bodě A (první záblesk) a končí v bodě
B (druhý záblesk). Pozorovatel na trati proto umístí do obou bodů
synchronizované hodiny
H1 a H2 . Na hodinách H1 je možné
určit začátek děje, na hodinách H2 jeho konec.
Rozdíl obou časových údajů delta t pak udává dobu trvání určitého děje, změřenou
hodinami, které jsou vzhledem k Zemi v klidu.
2.
Ve vlaku pohybujícím se vzhledem k Zemi rovnoměrně přímočaře konstantní rychlostí
v leží ve směru pohybu tyč. Pozorovatel ve vlaku měřením zjistil,
že tyč má délku l´. Vysvětlete, jak může změřit délku této tyče
pozorovatel na trati, vzhledem k němuž se tyč pohybuje rychlostí v.
Řešení
Zvolíme soustavu K spojenou se Zemí a soustavu K ´ spojenou s vlakem.
Tyč je vzhledem k soustavě K ´ v klidu a vzhledem k soustavě K
se pohybuje rychlostí v.
Pozorovatel ve vlaku může změřit délku tyče l´ obvyklým způsobem,
tj. porovnáním měřené tyče s délkovým normálem.
Pozorovatel na Zemi může změřit délku pohybující se tyče tak, že vyznačí na ose x okamžité
polohy koncových bodů tyče, zjistí jejich souřadnice x1 a x2
a délku tyče l v soustavě souřadnic K vypočte pomocí vztahu
v = x2 - x1.
Přitom je však nutné, aby poloha koncových bodů tyče na ose x byla v soustavě
K vyznačena současně. To lze realizovat např. pomocí synchronizovaných
hodin rozmístěných podél osy x.
3.
Auto záchranné služby vysílá při jízdě ulicemi města světelné signalizační záblesky.
Jsou tyto záblesky soumístné události?
Řešení
Zvolíme-li za
vztažnou soustavu Zemi, pak vzhledem k ní vznikají jednotlivé záblesky
na různých místech. Zvolíme-li však jako vztažnou soustavu jedoucí auto záchranné
služby, pak v této soustavě jsou všechny záblesky soumístné.
Z příkladu plyne, že bez udání vztažné soustavy nelze rozhodnout, zda určité události jsou či nejsou soumístné. Soumístnost událostí je tedy relativní pojem. Relativnost soumístnosti událostí je důsledkem relativnosti polohy bodu.
4.
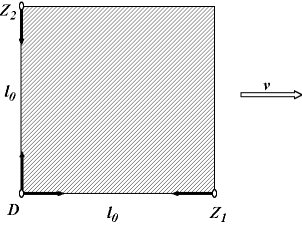
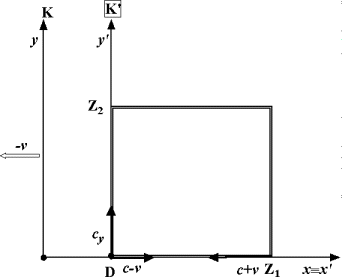
V klidné vodě jezera se pohybuje čtvercový vor o straně l0
konstantní rychlostí v (viz obrázek). Z bodu D
vyplují současně
dva plavci. První plave podél voru po dráze DZ1D, druhý po dráze
DZ2D. Oba se pohybují stálou rychlostí c < v
vzhledem k vodě. Který z obou plavců se vrátí do bodu D dříve?

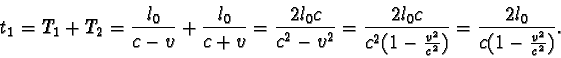
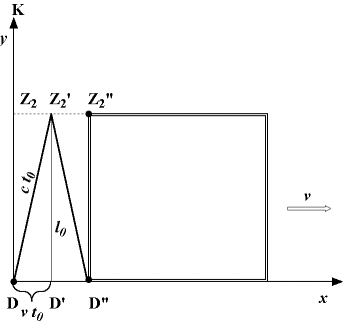
a tedy
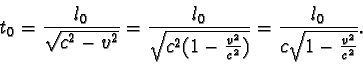
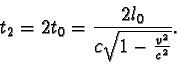
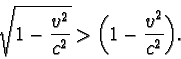
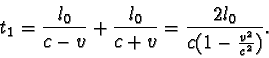
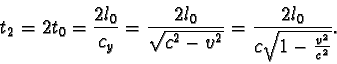
Všimněme si, že oba plavci se pohybují v soustavě spojené s vodou stejnými rychlostmi po různých dráhách, zatímco v soustavě voru se pohybují různými rychlostmi po stejných dráhách. Příklad s vorem je modelovým příkladem k Michelsonovu pokusu.
Příklady k procvičení - Úvodní pojmy
Začátek stránky
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Speciální teorie relativity, Jaroslav Joch © 2000