Příklady k pochopení - Relativistická dynamika

Příklady k pochopení
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika

Relativistická dynamika

1. Letadlo o klidové hmotnosti 20 t letí rychlostí 1 000 km.h^-1 vzhledem k Zemi. Vypočtěte přírustek jeho hmotnosti.

Řešení
Pro rychlost $v = 1 000 km.h^{-1} \doteq 0,3 km.s^{-1} \doteq 10^{-6}c$ dostáváme podle tabulek $\gamma = 1 + 5.10^{-13}$ ; přírustek hmotnosti letadla je tedy

$\begin{displaymath}\triangle m = m - m_{0} = m_{0}(\gamma - 1) = 2.10^{4}.5.10^{-13} kg = 10^{-8} kg = 10^{-2} mg. \end{displaymath}$

Výpočet ukazuje, proč v běžném životě nezjišťujeme přírustek hmotnosti tělesa při jeho rostoucí rychlosti. Při malých rychlostech oproti c je totiž přírustek hmotnosti velmi malý, takže hmotnost tělesa můžeme s dostatečnou přesností považovat za konstantní.

2. V urychlovači získal elektron rychlost v = 0,999 999 92c. Vypočtěte jeho relativistickou hmotnost a porovnejte ji s klidovou hmotností protonu m_p = 1,67.10^-27 kg. Klidová hmotnost elektronu m₀ = 9,1.10^-31 kg.

Řešení
Poněvadž $\beta = \frac{v}{c} = 0,999 999 92$ 0,999 999 92, je $1 - \beta = 8.10^{-8}$ a podle tabulek $\gamma = 2,5.10^{3}$ .
Pro hledanou relativistickou hmotnost elektronu m pak dostáváme m = gm₀ = 2,5.10³.9,1.10^-31 kg = 2,25.10^-27 kg. Hmotnost elektronu je při této rychlosti větší než klidová hmotnost protonu.

3. Ze vztahu m = gm₀ vyplývá, že urychlíme-li těleso o klidové hmotnosti 1kg na rychlost blízkou rychlosti světla, stává se jeho hmotnost nekonečně velkou. Znamená to, že by hmota tohoto tělesa při této rychlosti zaplnila celý vesmír?

Řešení
Tato představa není správná. Její vznik lze psychologicky snadno zdůvodnit, neboť např. víme, že železné těleso o hmotnosti 100 kg má stokrát větší objem než železné těleso o hmotnosti 1 kg, a to vede někdy k představě, že také při vzrůstu relativistické hmotnosti tělesa podle vztahu m = gm₀ roste bez omezení i jeho objem. Aplikovat však tuto úvahu na vzrůst relativistické hmotnosti podle uvedeného vztahu není správné, neboť zde hmotnost tělesa neroste zvětšením počtu částic, ale způsobem, který klasická fyzika nezná (tj. závislostí hmotnosti tělesa na jeho rychlosti). Jak již víme, objem tělesa se s jeho rostoucí rychlostí nejen nezvětšuje, ale naopak zmenšuje, poněvadž se kontrakcí délky, zkracují rozměry tělesa ve směru jeho pohybu; při rychlostech blížících se rychlosti světla c by se tyto rozměry blížily k nule. Tvrzení, že při velkých rychlostech roste hmotnost tělesa nade všechny meze, nelze tedy chápat tak, jako by se hmota tohoto tělěsa rozšířila na celý vesmír, ale tak, že urychlit toto těleso při tak velké rychlosti je prakticky nemožné; proto nemůžem žádné těleso s klidovou hmotností různou od nuly dosáhnout rychlosti světla nebo ji překročit.

4. Železný kvádr se vzhledem k soustavě souřadnic K pohybuje rychlostí 0,98c ve směru osy x tak, že jeho hrany jsou rovnoběžné se souřadnicovými osami této soustavy. Určete hustotu železa vzhledem k soustavě souřadnic K.

Řešení
Klidová hustota železa při rychlosti v = 0 je podle tabulek

$\begin{displaymath}\rho_{0} = \frac{m_{0}}{V_{0}} = \frac{m_{0}}{a_{0}b_{0}c_{0}} \doteq 7,8.10^{3} kg.m^{-3}.\end{displaymath}$

Hustotu železného kvádru, který se pohybuje vzhledem k pozorovateli rychlostí v, určíme ze vztahu

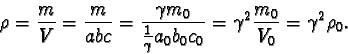
$\begin{displaymath}\rho = \frac{m}{V} = \frac{m}{abc} = \frac{\gamma m_{0}}{\f... ...}c_{0}} = \gamma^{2}\frac{m_{0}}{V_{0}} = \gamma^{2}\rho_{0}. \end{displaymath}$

Pro v = 0,98c je $\gamma \doteq 5,02^{2}.7,8.10^{3} kg.m^{-3} \doteq 200.10^{3} kg.m^{-3}.$ Hustota je stejně jako hmotnost nebo objem relativní veličina.

5. Odvoďte vztah pro hybnost fotonu $p = \frac{E}{c}$ , kde E = hn je energie fotonu a c rychlost světla. Při odvození tohoto vztahu využijte de Broglieho vztahu $p = \frac{h}{\lambda}$ , ve kterém p je hybnost částice, h je Plancova konstanta a l vlnová délka vlnění přiřazeného dané částici.

Řešení
Odvození vztahu $p= \frac{E}{c}$ je zřejmé ze zápisu

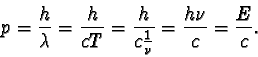
$\begin{displaymath}p = \frac{h}{\lambda} = \frac{h}{cT} = \frac{h}{c\frac{1}{\nu} } = \frac{h\nu}{c} = \frac{E}{c}.\end{displaymath}$

Hybnost fotonu se projevuje např. při srážkách fotonu s jinými částicemi. Při nich platí zákon zachování energie i zákon zachování hybnosti. Pro hybnost fotonu nelze použít vztah p = gm₀v, neboť foton se vždy pohybuje rychlostí světla a Lorentzův koeficient g nemá zřejmě pro v = c smysl (ve jmenovateli koeficientu by byla nula).

6. Těleso s klidovou hmotností m₀ se vzhledem k soustavě souřadnic K pohybuje ve směru osy x rychlostí v = 4/5c a narazí na těleso o stejné klidové hmotnosti, které je vzhledem k této soustavě v klidu. Předpokládejme, že srážka obou těles je dokonale nepružná. Vypočítejte vzhledem k soustavě K rychlost tělesa, které se vytvoří po srážce obou těles, a určete jeho klidovou hmotnost.

Řešení
Označme M₀ klidovou hmotnost tělesa, které by vzniklo po srážce obou těles, a w jeho rychlost v soustavě K. Vzhledem k tomu, že se těleso o klidové hmotnosti m₀ pohybuje rychlostí srovnatelnou s rychlostí světla, je třeba zákony zachování hmotnosti a hybnosti vyjádřit v relativistickém tvaru

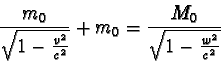
$\begin{displaymath}\frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}} } } + m_{0} = \frac{M_{0}}{\sqrt{1 - \frac{w^{2}}{c^{2}} } }\end{displaymath}$

(zákon zachování hmotnosti),

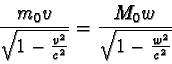
$\begin{displaymath}\frac{m_{0}v}{\sqrt{1 - \frac{v^{2}}{c^{2}} } } = \frac{M_{0}w}{\sqrt{1 - \frac{w^{2}}{c^{2}} } }\end{displaymath}$

(zákon zachování hybnosti). Po dosazení za $v = \frac{4}{5}c$ a po vyřešení obou rovnic dostáváme $w = \frac{1}{2}c$
a $M_{0} = \frac{4}{\sqrt{3} }m_{0}$ .

Z řešení vyplývá, že hledaná klidová hmotnost M₀ tělesa vzniklého po nepružné srážce se nerovná součtu klidových hmotností obou těles. Tento výsledek však plně odpovídá formulaci zákona zachování hmotnosti v relativistické fyzice, který platí jen pro relativistické hmotnosti. Další nutnou podmínkou pro jeho použití je izolovanost uvažované soustavy těles.

7. Dvě tělesa o stejných klidových hmotnostech m₀ se pohybují proti sobě opačně orientovanými rychlostmi v a -v. Po dokonale nepružné srážce obou těles vznikne jediné těleso, které je vzhledem k soustavě K v klidu. Vypočítejte, jak velkou klidovou hmotnost M₀ má toto těleso, a porovnejte ji se součtem klidových hmotností 2m₀.

Řešení
Soustavu dvou těles, pohybujících se proti sobě, můžeme považovat za izolovanou, a proto se podle zákona zachování hmotnosti celková hmotnost obou pohybujících se těles před srážkou musí rovnat hmotnosti tělesa, které vznikne po nepružné srážce; platí tedy 2m = M₀. Poněvadž m = gm₀ dostaneme po dosazení M₀ = 2gm₀. Vzhledem k tomu, že g > 1 je M₀ > 2m₀. Přírustek klidové hmotnosti tělesa, které vznikne po nepružné srážce, lze vypočítat z rovnice

$\triangle m = M_{0} - 2m_{0} = 2\gamma m_{0} - 2m_{0} = 2m_{0}(\gamma - 1)$ . Je-li $v \ll c$ , je $\gamma \doteq 1$ , $M_{0} \doteq 2m_{0}$ a $\triangle m = O$ ;
obecně však rovnice M₀ = 2m₀ neplatí. S neplatností zákona zachování klidových hmotností jsme se již setkali v předchozím příkladu.

8. Určete přírustek hmotnosti jednoho kilogramu vody při ohřátí z 0°C na 100°C.

Řešení
Měrná tepelná kapacita vody je přibližně 4,2.10³J.kg^-1.K^-1; proto se při ohřátí vody o hmotnosti 1kg o 100°C zvětší její vnitřní energie o $\triangle E \doteq 4,2.10^{5} J$ J. Pro přírustek hmotnosti Dm pak dostáváme

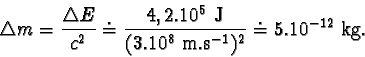
$\begin{displaymath}\triangle m = \frac{\triangle E}{c^{2}} \doteq \frac{4,2.10^{5} J}{(3.10^{8} m.s^{-1})^{2}} \doteq 5.10^{-12} kg.\end{displaymath}$

Energie, kterou dodáváme makroskopickým tělesům v běžném životě (např. při zahřívání tělesa, při zvětšování jeho rychlosti, apod.), je relativně malá, a proto je příslušný přírůstek hmotnosti ve srovnání s hmotností tělesa zanedbatelný. Díky tomu můžeme v běžném životě považovat hmotnost tělesa prakticky za konstantní a nezávislou na jeho energii.

9. Odvoďte vztah pro vazební energii jádra atomu.

Řešení
Protony a neutrony se v jádře atomu navzájem přitahují, a proto k rozdělení jádra na Z protonů a N neutronů je třeba jádru dodat určitou energii. Energie potřebná k rozložení jádra na volné nukleony se nazývá vazební energie jádra E_j. Soustava Z volných protonů a N volných neutronů má tedy větší energii než jádro atomu, které se z těchto částic skládá, a podle rovnice $\triangle m = \frac{E_{j}}{c^{2}}$ má také větší klidovou hmotnost. Rozdíl mezi klidovou hmotností volných nukleonů, z nichž se skládá jádro, a klidovou hmotností jádra atomu se nazývá hmotnostní úbytek Dm. Existence hmotnostního úbytku je v zřejmém rozporu s kasickou fyzikou, je však nutným důsledkem Einsteinovu vztahu mezi hmotností a energií. Z definice hmotnostního úbytku vyplývá vztah

Dm = Zm_p + Nm_n - m_j,

kde m_p je klidová hmotnost volného protonu, m_n klidová hmotnost volného neutronu a m_j klidová hmotnost jádra. Poněvadž klidové hmotnosti protonu, neutronu a jader atomů lze přesně změřit, lze podle předchozí rovnice určit hmotnostní úbytek Dm jádra atomu experimentálně. Vazební energii jádra atomu pak vypočteme z rovnice

E_j = Dmc² = (Zm_p + Nm_n - m_j)c².

10. Klidová hmotnost deuteronu (částice složené z protonu a neutronu) m_d je asi 3,343 3.10^-27 kg; klidové hmotnosti protonu a neutronu jsou m_p asi 1,672 6.10^-27 kg a m_n asi 1,674 9.10^-27 kg. Vysvětlete, proč je součet klidových hmotností protonu a neutronu větší než klidová hmotnost deuteronu, a z rozdílu těchto hmotností vypočtěte vazební energii deuteronu.

Řešení
Při oddělení protonu a neutronu je třeba vykonat práci, která se rovná vazební energii deuteronu (tj. energii potřebnou k oddělení protonu a neutronu). Soustava skládající se z volného protonu a neutronu má tedy větší energii než deuteron a podle rovnice $\triangle m = \frac{\triangle E}{c^{2}}$ má také větší klidovou hmotnost. Rozdíl mezi součtem klidových hmotností volného protonu a neutronu a klidovou hmotností deuteronu je hmotnostní úbytek deuteronu. Ze známého hmotnostního úbytku Dm lze pak vazební energii deuteronu E_j vypočítat z rovnice

$\begin{displaymath}E_{j} = \triangle mc^{2} = (m_{p} + m_{n} - m_{d})c^{2} = \end{displaymath}$
$\begin{displaymath}4,2.10^{-30}.(2,9979.10^{8})^{2} J \doteq 4.10^{-30}.9.10^{16} J = 3,6.10^{-13} J \doteq 2,2 MeV.\end{displaymath}$

11. Těleso má klidovou hmotnost m₀ = 1 kg. Určete jeho klidovou energii a porovnejte ji s energií, která se uvolní dokonalým spálením 1 kg uhlí o výhřevnosti H = 3.10⁷ J.kg^-1.

Řešení
Klidová energie tělesa o hmotnosti 1 kg je
E₀ = m₀c² = 1.9.10¹⁶ J = 9.10¹⁶ J. Spálením uhlí o hmotnosti 1 kg se uvolní energie E = 3.10⁷ J; poměr obou energií je tedy

$\frac{E_{0}}{E} = 3.10^{9}$ .

Z řešení příkladu je zřejmé, že těleso o hmotnosti 1 kg z jakékoli látky má obrovskou klidovou energii. Tato energie je asi z 99% určena klidovou energií částic, ze kterých se těleso skládá. Zbytek klidové energie je obsažen ve vazební energii jader atomů, v kinetické a potenciální energii molekul, v energii vzbuzených atomů, apod. Plné praktické využití celkové klidové energie tělesa však zatím není možné.

12. Elektron má klidovou hmotnost m₀ asi 9.10^-31 kg. Určete jeho klidovou energii.

Řešení

$\begin{displaymath}E_{0} = m_{0}c^{2} \doteq 9.10^{-31}.(3.10^{8})^{2} J = 8,1.10^{-14} J \doteq 0,51MeV.\end{displaymath}$

Klidová energie elektronu je 0,51 MeV.

13. Podle rovnice E = mc² má každý materiální objekt s celkovou energií E hmotnost m = E/c². Určete podle této rovnice hmotnost fotonu monofrekvenčního světla o vlnové délce l = 400 nm.

Řešení

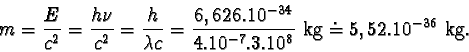
$\begin{displaymath}m = \frac{E}{c^{2}} = \frac{h\nu}{c^{2}} = \frac{h}{\lambda... ...6,626.10^{-34}}{4.10^{-7}.3.10^{8}} kg \doteq 5,52.10^{-36} kg.\end{displaymath}$

Hmotnost fotonu monofrekvenčního světla o vlnové délce l = 400 nm je 5,52.10^-36 kg. Klidová hmotnost fotonu m₀ je rovna nule. Z řešení příkladu plyne, že relativistická hmotnost fotonu m pohybujícího se ve vakuu rychlostí světla je vždy různá od nuly. Foton se tedy chová jako částice, která má energii $E = h\nu$ , hmotnost $m = \frac{E}{c^{2}}$ a hybnost $p = \frac{E}{c}$ .

14. Hustota zářivého toku Slunce ve střední vzdálenosti Země od Slunce r = 1,5.10¹¹ m je určena solární konstantou K = 1 327 W.m^-2. Zjistěte celkovou energii vyzářenou Sluncem za jednu sekundu a úbytek hmotnosti Slunce za tuto dobu.

Řešení
Slunce vyzáří za dobu Dt = 1 s energii

$\begin{displaymath}\triangle E = 4\pi r^{2}K\triangle t \doteq 4.3,14.1,5^{2}.10^{22}.1,327.10^{3}.1 J \doteq 3,75.10^{26} J.\end{displaymath}$

Úbytek hmotnosti Slunce za tuto dobu je tedy

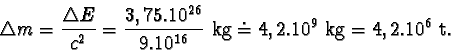
$\begin{displaymath}\triangle m = \frac{\triangle E}{c^{2}} = \frac{3,75.10^{26}}{9.10^{16}} kg \doteq 4,2.10^{9} kg = 4,2.10^{6} t.\end{displaymath}$

Výpočtem snadno zjistíme, že úbytek hmotnosti Slunce za jeden rok je asi 1,3.10¹⁴ t. Tento úbytek je ale v porovnání s celkovou hmotností Slunce velmi malý.

15. Energie částice E = mc² a její hybnost p = mv jsou relativní veličiny; při přechodu od jedné inerciální vztažné soustavy k druhé se obě veličiny mění (nejsou invariantní). Dokažte však, že veličina E² - p²c² je ve speciální teorii relativity invariantní.

Řešení
Důkaz provedeme přímým výpočtem výrazu E² - p²c². Užitím vztahů E = mc², p = mv a m = gm₀ dostáváme

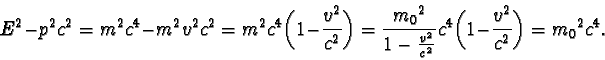
$\begin{displaymath}E^{2} - p^{2}c^{2} = m^{2}c^{4} - m^{2}v^{2}c^{2} = m^{2}c^{4... ...} \biggl(1 - \frac{v^{2}}{c^{2}} \biggr) = {m_{0}}^{2}c^{4}.\end{displaymath}$

Vztah

E² - p²c² = m₀²c⁴

se nazývá relativistický vztah mezi energií a hybností. Poněvadž pravá strana této rovnice m₀²c⁴ je invariantní (m₀ a c jsou invariantní veličiny), musí být invariantní také veličina E² - p²c². To znamená, že ve všech inerciálních vztažných soustavách má veličina E² - p²c² tutéž hodnotu m₀²c⁴, i když veličiny E a p mají v různých vztažných soustavách různou hodnotu.

16. Vypočtěte kinetickou energii, kterou by měla raketa o klidové hmotnosti 10 tun, kdyby se pohybovala rychlostí 0,98c.

Řešení

$\begin{displaymath}E_{k} = m_{0}c^{2}(\gamma - 1) \doteq 10^{4}.9.10^{16}(5 - 1) J = 3,6.10^{21} J = 10^{15} kWh.\end{displaymath}$

Při vypuštění rakety by si však tato vyžádala ještě další energii k vymanění ze zemské přitažlivosti a k zabrzdění u cíle. Velkou energii by si vyžádal také zpětný návrat rakety. Lety s tak velkou rychlostí tedy nejsou prozatím možné.

17. Jakou práci je třeba vykonat, aby částice s klidovou hmotností m₀ zvětšila svou rychlost z 0,6c na 0,8c?

Řešení
Hledaná práce se rovná rozdílu kinetických energií částice při rychlostech 0,8c a 0,6c

$\begin{displaymath}W = E_{k2} - E_{k1} = m_{0}c^{2}(\gamma_{2} - 1) - m_{0}c^{2}(\gamma_{1} - 1) = m_{0}c^{2}(\gamma_{2} - \gamma_{1}).\end{displaymath}$

Podle tabulek odpovídá rychlostem v₂ = 0,8c a v₁ = 0,6c Lorentzův koeficient g₂ = 1,667 a g₁ = 1,250. Pro hledanou práci proto dostáváme

$\begin{displaymath}W = m_{0}c^{2}(1,667 - 1,250) \doteq 0,42 m_{0}c^{2}.\end{displaymath}$

Podle klasické fyziky bychom hledanou práci vypočetli ze vztahu

$\begin{displaymath}W = E_{k2} - E_{k1} = \frac{1}{2}m_{0}{v_{2}}^{2} - \frac{1}{... ... \frac{1}{2}m_{0}(0,8^{2} - 0,6^{2})c^{2} = 0,14m_{0}c^{2}.\end{displaymath}$

Z výsledku vidíme, že klasický vztah pro kinetickou energii není použitelný při rychlostech srovnatelných s rychlostí světla.

18. Urychlovač protonů poskytuje protony s kinetickou energií přibližně 500 GeV. Vypočtěte, kolikrát v tomto urychlovači vzroste hmotnost protonů a jaké maximální rychlosti protony dosáhnou. Klidová hmotnost protonu m₀ je asi 1,67.10^-27 kg, klidová energie protonu E₀ asi 0,938 GeV.

Řešení
Celková energie protonu E = mc² = gm₀ c² je rovna součtu jeho klidové energie E₀ = m₀c² a energie kinetické E_k. Z rovnice gm₀c² = m₀c² + E_k pak dostáváme

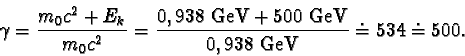
$\begin{displaymath}\gamma = \frac{m_{0}c^{2} + E_{k}}{m_{0}c^{2}} = \frac{0,938 GeV + 500 GeV}{0,938 GeV} \doteq 534 \doteq 500.\end{displaymath}$

Z rovnice $\gamma = \frac{m}{m_{0}} \doteq 500$ vyplývá, že hmotnost protonu s klidovou energií 500 GeV je přibližně 500krát větší než jeho hmotnost klidová. Hodnotě Lorentzova koeficientu $\gamma \doteq 500$ pak odpovídá rychlost $v \doteq \mbox{ 0,999 998}c$ .

19. Vraťte se k řešení př.7 a vysvětlete, proč při nepružné srážce dvou těles o stejných klidových hmotnostech m₀, pohybujících se proti sobě opačně orientovanými rychlostmi v a -v, neplatí zákon zachování klidových hmotností.

Řešení
Předokládejme, že obě tělesa o klidových hmotnostech m₀ jsou nejprve vzhledem k vztažné soustavě K v klidu; celková energie této soustavy je pak totožná s její klidovou energií E₀ = 2m₀c². Při uvádění těchto těles do pohybu s rychlostmi v
a -v musíme vykonat práci, která se rovná přírustku kinetické energie soustavy DE_k = 2m₀c². Poněvadž kinetická energie soustavy vzroste při tomto ději o DE_k a po srážce se obě tělesa zastaví, zvětší se po srážce podle zákona zachování energie jejich klidová energie o DE₀ = DE_k a tím se současně zvětší i jejich klidová hmotnost o

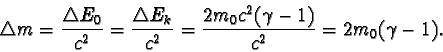
$\begin{displaymath}\triangle m = \frac{ \triangle E_{0} }{c^{2}} = \frac{ \trian... ... = \frac{2m_{0}c^{2}(\gamma - 1)}{c^{2}} = 2m_{0}(\gamma - 1).\end{displaymath}$

20. Jaké rychlosti dosáhne elektron v elektrickém poli, projde-li mezi dvěma body, mezi kterými je napětí U? Počáteční rychlost elektronu je rovna nule.

Řešení
Pro malé hodnoty urychlujícího napětí U, pro které $v \ll c$ , lze hledanou rychlost v vypočítat ze vztahu $\frac{1}{2}m_{0}v^{2} = eU$ , z něhož vyplývá

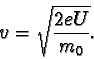
$\begin{displaymath}v = \sqrt{\frac{2eU}{m_{0}} }.\end{displaymath}$

Při větším napětím U mohou však elektrony v elektrickém poli získat i velmi velkou rychlost $v \to c$ , a proto je třeba kinetickou energii elektronů obecně vyjádřit relativistickým vztahem E_k = m₀c² (g - 1). Ze vztahu mezi kinetickou energií elektronu a prací vykonanou elektrickým polem

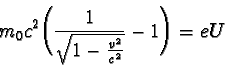
$\begin{displaymath}m_{0}c^{2} \Biggl(\frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}} } } - 1 \Biggr) = eU\end{displaymath}$

po úpravách pak dostáváme pro hledanou rychlost v vztah

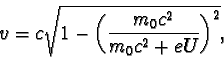
$\begin{displaymath}v = c\sqrt{1 - \biggl(\frac{m_{0}c^{2}}{m_{0}c^{2} + eU} \biggr)^{2} },\end{displaymath}$

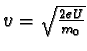který platí pro libovolná urychlující napětí U. Jestliže $U \to \infty$ , blíží se hodnota zlomku pod odmocninou k nule a rychlost elektronu v se blíží rychlosti světla ( $v \to c$ ). Odtud vyplývá, že při sebevětším urychlovacím napětí U nemůže rychlost elektronu překročit rychlost světla ve vakuu. Podle klasického vztahu $v = \sqrt{\frac{2eU}{m_{0}} }$ by se rychlost elektronu s rostoucím napětím neomezeně zvyšovala. Upravme vztah pro rychlost elektronu urychlovaného elektrickým polem na tvar

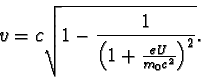
$\begin{displaymath}v = c\sqrt{1 - \frac{1}{ \Bigl(1 + \frac{eU}{m_{0}c^{2}} \Bigr)^{2} } }.\end{displaymath}$

je-li

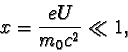
$\begin{displaymath}x = \frac{eU}{m_{0}c^{2}} \ll 1,\end{displaymath}$

lze složený zlomek pod odmocninou upravit užitím přibližného vztahu

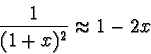
$\begin{displaymath}\frac{1}{(1 + x)^{2}} \approx 1 - 2x\end{displaymath}$

na tvar

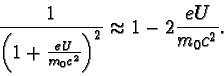
$\begin{displaymath}\frac{1}{\biggl(1 + \frac{eU}{m_{0}c^{2}} \biggr)^{2} } \approx 1 - 2\frac{eU}{m_{0}c^{2}}.\end{displaymath}$

Po dosazení tohoto výrazu do vztahu pro rychlost v pak dostáváme

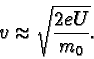
$\begin{displaymath}v \approx \sqrt{\frac{2eU}{m_{0}} }.\end{displaymath}$

Při malých napětích U, při nichž $eU \ll m_{0}c^{2}$ , lze tedy rychlost elektronu v vypočítat užitím zákonů klasické fyziky.

Příklady k procvičení - Dynamika

Začátek stránky
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika