Dynamika
předchozí - Obsah - další
Hmotnost - Hybnost - Energie a hmotnost - Kinetická energie

Relativistická hmotnost

Podle zákonů klasické fyziky se částice, na niž působí konstantní síla, pohybuje pohybem rovnoměrně zrychleným. Z rovnice v = at pak plyne, že rychlost této částice by neustále rostla a za dostatečně dlouhou dobu by překročila rychlost světla ve vakuu c. To však podle speciální teorie relativity není možné, a proto je nutné klasickou dynamiku, která je dostatečně experimentálně ověřena při rychlostech mnohem menších než rychlost světla c, nahradit relativistickou dynamikou platící obecně při libovolných rychlostech v.

Podle klasické fyziky je hmotnost m daného tělesa konstantní a nezávislá na jeho rychlosti. Einstein však předpokládal, že hmotnost každého tělesa se s jeho rostoucí rychlostí zvětšuje. Pro tento jev odvodil pomocí jednoduchého myšlenkového pokusu také kvantitativní vztah.

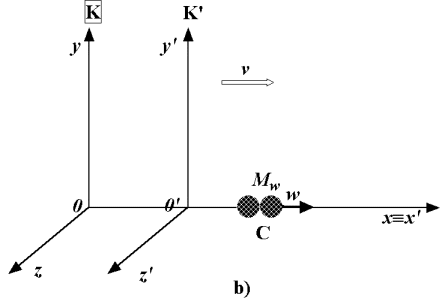
Uvažoval při tom nepružnou srážku dvou stejných koulí (tzn. že v klidové vztažné soustavě mají stejný objem i hmotnost) a předpokládal, že hmotnost každého tělesa závisí na jeho rychlosti vzhledem ke zvolené inerciální vztažné soustavě a že v libovolné vztažné soustavě platí zákon zachování hmotnosti a hybnosti. Předpokládejme, že koule A se vzhledem k vztažné soustavě K pohybuje rychlostí v a narazí na kouli B, která je vzhledem k soustavě K v klidu (obr a). Hmotnost koule A označíme mv a hmotnost koule B, která je v klidu, označíme m0. V důsledku nepružné srážky vznikne výsledné těleso C, které se pohybuje vzhledem k soustvě K rychlostí w (obr b). Hmotnost tohoto tělesa označíme Mw. Podle zákona zachování hybnosti se hybnost soustavy před srážkou bude rovnat hybnosti soustavy po srážce. Platí proto vztah mvv = Mww. Zákon zachování hmotnosti lze při tomto ději vyjádřit ve tvaru mv + m0 = Mw.

Uvažujeme-li tutéž situaci z hlediska vztažné soustavy K ´, která se pohybuje vzhledem k soustavě K v kladném směru osy x rychlostí v, tj. rychlostí pohybu koule A vzhledem k soustavě K, dochází k obdobnému jevu, jako v předchozím případě. Koule A je v soustavě K ´ v klidu a koule B se pohybuje rychlostí -v. Tato situace je symetrická s předešlou, a proto se výsledené těleso C bude vzhledem k soustavě K ´ pohybovat rychlostí -w.

K nalezení vztahu mezi rychlostmi v a w využijeme pro výsledné těleso C relativistický vztah pro skládání rychlostí

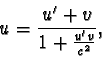
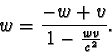
\begin{displaymath}u = \frac {u' + v}{1 + \frac {u'v}{c^2} }, \end{displaymath}

kde u´ je velikost rychlosti výsledného tělesa C vzhledem k soustavě K ´, u je velikost rychlosti téhož tělesa vzhledem k soustavě K a v velikost rychlosti soustavy K ´ vzhledem k soustavě K. V našem případě však položíme u´ = -w a u = w. Relativistický vztah pro skládání rychlostí tak přejde na tvar

\begin{displaymath}w = \frac {-w + v}{1 - \frac {wv}{c^2} }. \end{displaymath}

Při použití výše uvedených vztahů pro zachování hybnosti a hmotnosti dostáváme

mvv = (mv + m0)w

a po vyjádření velikosti rychlosti w, ji dosadíme do upravené rovnice pro skládání rychlostí

\begin{displaymath}w \biggl(1 - \frac {wv}{c^2} \biggr) = v - w. \end{displaymath}

Tím dostáváme
\begin{displaymath}\frac {m_{v}v}{m_{v} + m_{0}} \biggl[1 - \frac {m_{v}v^2}{c^2(m_{v} + m_{0})} \biggr] = v - \frac {m_{v}v}{m_{v} + m_{0}} \end{displaymath}

a odtud potom několika úpravami dospějeme již k hledané závislosti hmotnosti mv na rychlosti v

mv2(c2 - v2) = m02c2,

\begin{displaymath}m_{v} = \frac {m_{0}}{ \sqrt {1 - \frac {v^2}{c^2} } }, \end{displaymath}

nebo stručněji $m_{v} = \gamma m_{0}$, kde veličinu mv nazýváme relativistická hmotnost tělesa nebo částice .

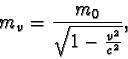
Je-li těleso vzhledem k vztažné soustavě v klidu, pak z uvedeného vztahu dostáváme m = m0. Relativistickou hmotnost tělesa m0 proto nazýváme klidová hmotnost tělesa. Tato je pro dané těleso stejná ve všech vztažných soustavách, a proto říkáme že je to invariantní veličina. Ze vztahu je také zřejmé, že s rostoucí rychlostí tělesa se jeho relativistická hmotnost také zvětšuje, přičemž při rychlostech blížících se rychlosti světla roste jeho relativistická hmotnost nade všechny meze. Tím můžeme také vysvětit, proč žádná částice s nenulovou klidovou hmotností nemůže dosáhnout rychlosti světla.

Z výše uvedeného vztahu dále také plyne, že relativistická hmotnost tělesa či částice je relativní veličina závislá na uvažované vztažné soustavě. Relativistická hmotnost tedy není "mírou množství látky obsažené v tělese", jako setrvačná hmotnost v klasické fyzice, ale jde o dynamickou veličinu.

Pro relativistickou hmotnost samozřejmě také platí zákon zachování hmotnosti, který říká, že celková relativistická hmotnost izolované soustavy těles zůstává při všech dějích probíhajících v této soustavě konstantní.
Uvedený zákon i předchozí vztah byly mnohokrát potvrzeny v urychlovačích částic při pokusech s jejich srážkami.

Příklady k lepšímu pochopení - Příklady k procvičení

Začátek stránky
předchozí - Obsah - další
Hmotnost - Hybnost - Energie a hmotnost - Kinetická energie

Speciální teorie relativity, Jaroslav Joch © 2000