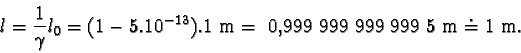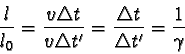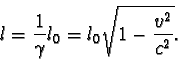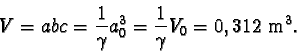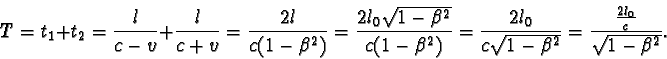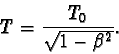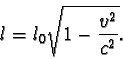Příklady k pochopení
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Kontrakce délky
1.
Na kosmické lodi vzdalující se od Země konstantní rychlostí je umístěna ve směru pohybu
tyč o
vlastní délce 1 m.
a) Jaká je délka této tyče pro pozorovatele na Zemi, jestliže se loď vzdaluje rychlostí
0,1c?
b) Je možné, aby tyč, která má na kosmické lodi délku 1 m, měla pro pozorovatele na Zemi
délku 1 mm?
Řešení
a) Vlastní délka tyče je
l0 = 1 m.
Délka této tyče vzhledem k Zemi je
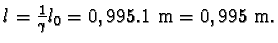
b) Z rovnice
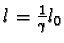 ,
kde
l =10-3 m a l0 = 1 m, dostáváme
,
kde
l =10-3 m a l0 = 1 m, dostáváme
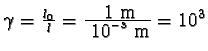 a pomocí tabulek pak
a pomocí tabulek pak
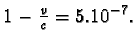 Odtud vyplývá, že
Odtud vyplývá, že
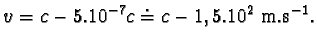 Tyč, která má na kosmické lodi délku 1 m, má vzhledem k Zemi délku 1 mm, jestliže
se pohybuje rychlostí jen o 150 m.s-1 menší, než je rychlost světla.
Tyč, která má na kosmické lodi délku 1 m, má vzhledem k Zemi délku 1 mm, jestliže
se pohybuje rychlostí jen o 150 m.s-1 menší, než je rychlost světla.
2.
V letadle letícím rychlostí 1 000 km.h-1 leží ve směru jeho letu tyč o vlastní
délce 1 m.
Jaká je délka této tyče vzhledem k Zemi?
Řešení
Pro rychlost
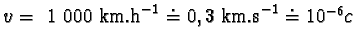 dostáváme
dostáváme
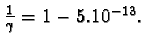 Hledaná délka l je tedy
Hledaná délka l je tedy
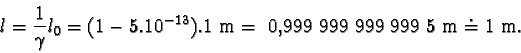
Délka tyče vzhledem k Zemi je tedy s velkou přesností opět 1 m.
Příklad ukazuje, že kontrakce délek se při rychlostech dopravních prostředků prakticky
neprojevuje. Tím lze vysvětlit, proč si každý z nás vytváří již v mládí představu
o absolutnosti délky.
3.
Délku pohybujícího se vlaku můžeme změřit také tak, že změříme dobu
Dt, po kterou kolem nás vlak projíždí stálou
rychlostí v, a délku vlaku pak vypočítáme z rovnice
l = vDt. Využijte tohoto způsobu měření délky
k odvození
vztahu pro kontrakci délek.
Řešení
Označme vztažnou soustavu, v níž je pozorovatel s hodinami H, symbolem K,
a klidovou vztažnou soustavu tyče označme K ´. Tyč, která se pohybuje vzhledem
k soustavě K rychlostí v, má v této soustavě délku
l = vDt.
Z hlediska pozorovatele v soustavě K ´ je tyč v klidu a hodiny H se pohybují
od koncového bodu tyče B k počátečnímu bodu A rychlostí
-v. Při tom urazí dráhu
l0 = vDt´
kde l0 je vlastní délka tyče.
Jaký vztah je mezi časovými intervaly Dt a
Dt´? Při pohybu tyče vzhledem
k soustavě K projde kolem hodin H nejdříve bod B a potom bod A.
Obě události jsou v této soustavě soumístné a časový interval mezi těmito událostmi
Dt změříme na hodinách H,
které jsou v soustavě K v klidu. Proto je Dt
vlastní čas, který uplyne mezi danými událostmi. Veličina
Dt´ je časový interval mezi stejnými událostmi měřený
v soustavě K ´, vzhedem k níž se hodiny H pohybují. V klasické fyzice by
platilo
Dt = Dt´,
ve speciální teorii relativity však mezi nimi platí vztah
Dt´ = gDt.
Pro poměr délek l a l0 pak z předchozích rovnic dostáváme
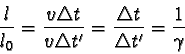
a odtud
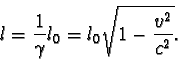
Z příkladu vyplývá, že i při odlišných způsobech měření délky tyče dostaneme tentýž vztah
pro kontrakci délek.
4.
Těleso, které má v klidové soustavě tvar krychle, se pohybuje ve směru osy x
rovnoměrně přímočaře rychlostí v kolmou na stěnu krychle.
Velikost rychlosti
krychle je v = 0,95c, klidová délka její hrany a0 = 1 m.
Určete objem tělesa ve vztažné soustavě K, vzhledem k níž se těleso pohybuje rychlostí
v.
Řešení
Krychle má v klidové vztažné soustavě K ´ objem
V0 = a03. Hrana tělesa ve směru jeho pohybu
je v soustavě K kratší než v soustavě K ´ a u příčných rozměrů kontrakce
nenastává.
Z hlediska pozorovatele v soustavě K je tedy pohybující se těleso kvádr o objemu
V = abc.
Poněvadž a = a0, b = a0 a
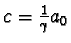 ,
je hledaný objem kvádru
,
je hledaný objem kvádru
Zpříkladu vyplývá, že tvar tělesa a jeho objem jsou vzhledem k volbě vztažné soustavy
relativní.
5.
Světelné hodiny
o délce l0 jsou orientovány paralelně ke směru svého
pohybu a pohybují se vzhledem k soustavě K ve směru osy x rychlostí
v.
Vypočtěte periodu T0 světelných hodin v jejich klidové soustavě K ´
a periodu T těchto hodin v soustavě K.
Jaký je vztah mezi těmito periodami?
Řešení
Pro pozorovatele v soustavě K ´ pohybujícího se společně se světelnými hodinami
se světlo
dostane od zrcátka Z1 k zrcátku Z2 a nazpět za dobu
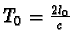 ,
kde l0 je vlastní délka světelných hodin.
Z hlediska pozorovatele v soustavě K, vzhledem k němuž se hodiny pohybují rychlostí
v, mají světelné hodiny kratší délku
,
kde l0 je vlastní délka světelných hodin.
Z hlediska pozorovatele v soustavě K, vzhledem k němuž se hodiny pohybují rychlostí
v, mají světelné hodiny kratší délku
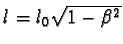 .
Za dobu t1, za kterou světlo přejde od zrcátka Z1
k zrcátku Z2 , se hodiny posunou o vt1, takže světelný
paprsek urazí ve směru pohybu hodin dráhu
.
Za dobu t1, za kterou světlo přejde od zrcátka Z1
k zrcátku Z2 , se hodiny posunou o vt1, takže světelný
paprsek urazí ve směru pohybu hodin dráhu
ct1 = l + vt1.
Dobu, za kterou se vrátí od zrcátka Z2 k zrcátku Z1,
označíme t2. Za tuto dobu se zrcátko Z1 posune vstříc
vracejícímu se paprsku o dráhu vt2, takže světlo urazí kratší dráhu
ct2 = l - vt2.
Perioda T světelných hodin vzhledem k soustavě K je tedy
Porovnáním period T a T0 dostáváme pak
Odvozený vztah mezi periodami T a T0 je stejný jako vztah
pro světelné hodiny pohybující se kolmo ke své ose. To je však samozřejmé, neboť podle
principu relativity se všechny hodiny umístěné v soustavě K ´ musí v soustavě K
zpomalovat stejně. Tento vztah musí ze stejného důvodu platit i pro světelné hodiny,
jejichž osa svírá s osou x libovolný úhel. V opačném případě by pozorovatel v uzavřené
soustavě K ´ mohl porovnáním chodu různě orientovaných hodin zjistit, že se jeho
soustava pohybuje rovnoměrně přímočaře, což by bylo v rozporu s principem relativity.
6.
Vysvětlete výsledek
Michelsonova pokusu
z hlediska speciální teorie relativity.
Při tom volte za vztažnou soustavu nejprve Zemi a pak libovolnou jinou
inerciální
vztažnou soustavu, v níž se Michelsonův interferometr pohybuje ve
směru svého ramena.
Řešení
Připomeňme si, že Michelsonův přístroj je v podstatě dvojice světelných hodin
s osami navzájem kolmými. Výklad Michelsonova pokusu v zemské vztažné soustavě jsme
již podali. Obě ramena interferometru mají vzhledem k Zemi stejnou délku
l0, takže světlo, které se šíří ve směru obou ramen stejnou rychlostí
c, se vrátí po odrazu od obou zrcátek zpět za stejně dlouhou dobu
 Pohybuje-li se Michelsonův interferometr vzhledem k libovolné vztažné soustavě K
ve směru ramena MZ1, pak délka tohoto ramena v soustavě K je
Pohybuje-li se Michelsonův interferometr vzhledem k libovolné vztažné soustavě K
ve směru ramena MZ1, pak délka tohoto ramena v soustavě K je
délka druhého ramena MZ2 se nemění. Světelný paprsek se šíří vzhledem
k soustavě K rychlostí c a dráhu v ramenu MZ1 směrem
k zrcátku a nazpět urazí za dobu
vypočtenou již v předcházejícím příkladu.
Světlo v druhém ramenu MZ2 urazí vzhledem k soustavě K dráhu
DZ'2D'' za dobu T2, pro niž podle Pythagorovy
věty platí
a odtud plyne
Porovnáním obou výrazů dostáváme
T1 = T2. Oba paprsky se vrátí současně.
7.
Vysvětlete, zda kosmonaut na kosmické lodi pohybující se vzhledem k Zemi rychlostí
blízkou rychlosti světla může pozorovat u předmětů rozmístěných na lodi kontrakci
jejich podélných rozměrů.
Řešení
Předměty na kosmické lodi jsou vzhledm k ní buď v klidu, anebo se pohybují jen
velmi malou rychlostí. Ze vztahu pro kontrakci délek
pak vyplývá l = l0, tzn. že pro pozorovatele na lodi kontrakce délek
u předmětů v lodi rozmístěných nenastává. Stejný závěr vyplývá z principu relativity,
neboť měření délek předmětů, které jsou vzhledem k lodi v klidu, musí na lodi probíhat
stejně jako obdobné měření v zemské laboratoři.
8.
Dvě rovnoběžné tyče MN a M´N´ mají stejnou vlastní délku
l0 = 1 m. Tyč MN je v klidu vzhledem k soustavě K,
tyč M´N´ se vzhledem k této soustavě pohybuje rychlostí o velikosti
v = 0,6c. Určete časový interval, který uplyne v soustavě
K mezi ztotožněním levých a pravých konců obou tyčí.
Řešení
Samozřejmě platí
l0 - 1 = vDt.
Odtud dostáváme
Mezi ztotožněním levých a pravých konců obou tyčí uplyne časový
interval 1,1 ns.
Příklady k procvičení - Kontrakce délky
Začátek stránky
předchozí - Obsah - další
Příklady - k pochopení / k procvičení / řešení - Úvodní pojmy - Galileiho transformace - Michelsonův pokus - Postuláty - Relativnost současnosti - Dilatace času - Kontrakce délky - Lorentzova transformace - Skládání rychlostí - Dynamika
Speciální teorie relativity, Jaroslav Joch © 2000
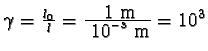 a pomocí tabulek pak
a pomocí tabulek pak